Effective Decision Theory
Lessons from Physics for Practical Rationality
Introduction
Decision-making under uncertainty often runs into paradoxes like Pascal’s Mugging or the St. Petersburg paradox, where extremely improbable yet high-impact outcomes dominate rational analysis.[1][2] Traditional Expected Utility Theory (EUT) struggles with these scenarios, demanding a practical solution. Here, physics provides an insightful analogy: Effective Field Theory (EFT).[3] Drawing on EFT, we introduce an analogous framework—Effective Decision Theory (EDT)—to improve decision-making under extreme uncertainty.
What is Effective Field Theory?
In physics, Effective Field Theory simplifies complex theories by explicitly ignoring phenomena occurring beyond a certain energy scale. It acknowledges the theoretical existence of high-energy events but pragmatically discounts them because they have negligible observable effects at accessible energies.[3]
Effective Decision Theory by Analogy
EDT adapts this principle to decision theory by introducing a probability cutoff below which outcomes are systematically ignored. This prevents improbable but catastrophic outcomes from irrationally skewing decisions.[4]
Core Principles of EDT:
Practical Probability Threshold:
EDT sets a defined threshold below which probabilities are treated as effectively zero.
This cutoff maintains rationality by preventing negligible-probability scenarios from dominating analysis.
Contextual Adaptation:
Like EFT’s energy scale cutoff, EDT’s probability cutoff can vary depending on the decision context, available information, or stakes involved.
Coherence with Practicality:
EDT maintains formal coherence within the defined probability domain, intentionally sacrificing theoretical completeness for practical effectiveness.
Justifying a Probability Cutoff
A probability cutoff is justified by the recognition that extremely low probabilities typically involve high epistemic uncertainty, modeling ambiguity, or unreliable data. Ignoring these probabilities does not deny their theoretical existence but acknowledges their practical irrelevance.[2][4]
Integrating EDT into Decision-Making
To use EDT effectively:
Explicitly choose and document the probability cutoff based on epistemic limits, practical stakes, and available data quality.
Use EDT transparently, facilitating clear, accountable decision-making.
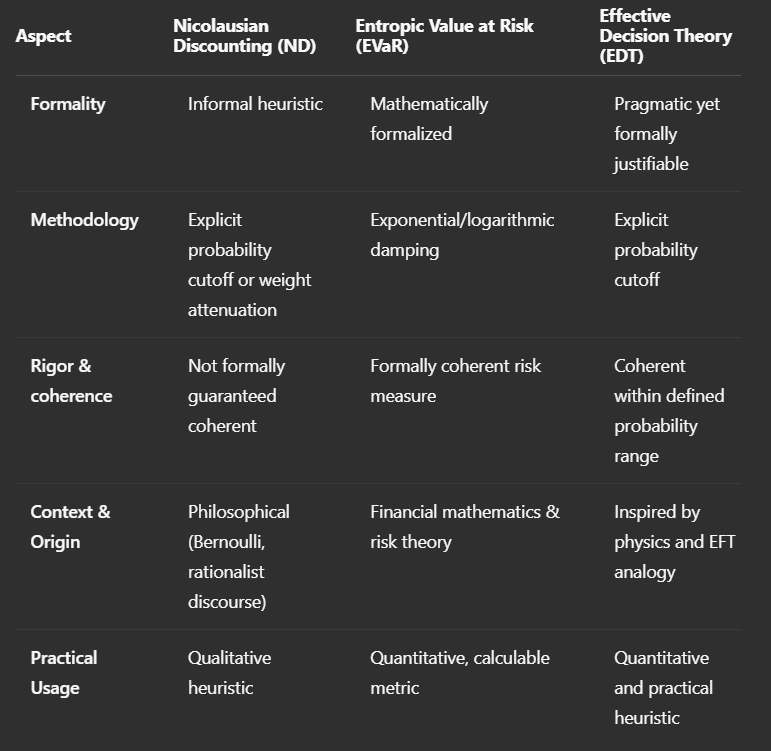
Relationship to Existing Approaches
Nicolausian Discounting: EDT formalizes the heuristic concept of explicitly discounting small probabilities, historically linked to Nicolaus Bernoulli’s St. Petersburg paradox.[1][4]
Entropic Value at Risk (EVaR): A coherent quantitative measure that can complement EDT by assessing risk within EDT's effective probability range.[5]
Challenges and Open Questions
Determining a rigorous method for selecting the optimal probability threshold.
Developing adaptive frameworks that dynamically adjust thresholds as conditions change.
Ensuring formal coherence of EDT within rigorous decision theory frameworks.
Conclusion
Effective Decision Theory provides a principled, practical solution inspired by physics to handle paradoxes that challenge classical expected utility theory. By adopting this framework, decision-makers can better navigate the complexities of real-world uncertainty without succumbing to paralysis by improbable catastrophes.
References
Bernoulli, Nicolaus. "The St. Petersburg paradox" (1713).
Bostrom, Nick. "Pascal's Mugging." Analysis 69, no. 3 (2009): 443-445.
Burgess, C.P. "Introduction to Effective Field Theory." Annual Review of Nuclear and Particle Science 57 (2007): 329-362.
Monton, Bradley. "How to Avoid Maximizing Expected Utility." Philosophers' Imprint 19, no. 18 (2019).
Ahmadi-Javid, Amir. "Entropic Value-at-Risk: A New Coherent Risk Measure." Journal of Optimization Theory and Applications 155, no. 3 (2012): 1105-1123.