Truth Machines
From Tarski to Gödel to Conditionalism
1. Syntax Without Meaning
Turing showed that a computation is a finite mechanical process operating on symbols according to formal rules. Crucially, those symbols are syntactic tokens—they have structure but no intrinsic semantics. A Turing machine can manipulate “0011” and “⊢P→Q” identically, because from the machine’s standpoint, both are mere patterns in a tape alphabet. This is the original schism of logic: computation explains form, not meaning.
2. Tarski’s Bridge
Alfred Tarski introduced the formal definition of truth:
A statement ‘P’ is true under an interpretation I if and only if P
holds in the model I.
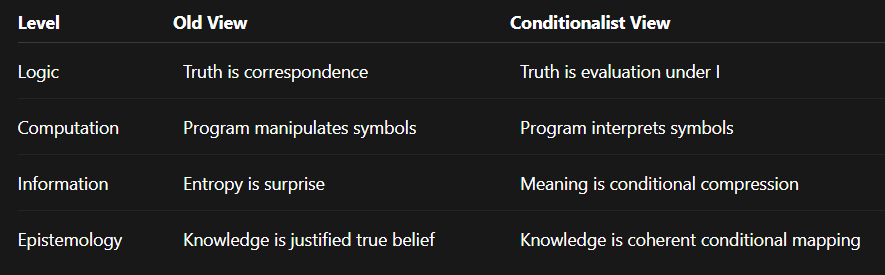
That single clause encodes Conditionalism avant la lettre. Truth is not absolute; it is evaluated relative to an interpretation. Even “Snow is white” is only true in English, given that “snow” refers to frozen precipitation and “white” denotes a spectral range of reflected light.
Formally, truth is conditional on interpretation:
Once the interpreter (I) is explicit, computation can evaluate such conditions.
3. Gödel and the Limits of Absoluteness
Kurt Gödel proved that any sufficiently expressive formal system contains true statements unprovable within the system itself. What this exposes is semantic dependency: the truth of certain propositions depends on an interpretation that cannot be fully captured by the system’s syntactic rules.
Chaitin later tightened this insight using algorithmic information theory: the boundary of provability coincides with the boundary of compressibility. Truths that exceed the system’s descriptive capacity cannot be generated by it. In both cases, the lesson is the same: no system carries its own semantics; interpretation leaks out of syntax.
4. Computation as Interpretation
Now observe the inversion: a computation is itself an interpretive act. Given input data P and a program I, the machine produces an output O = I(P). Semantically, I interprets P. Every evaluation—whether of arithmetic, logic, or natural language—is a mapping from pattern to meaning under some interpreter. Change the program, change the meaning.
Conditionalism rendered operational:
There are no absolute truths, only consistent interpreter–pattern pairs.
5. Information, Compression, and Meaning
Shannon stripped semantics from information theory intentionally: entropy measures surprise, not meaning. Chaitin’s incompressible numbers show why: most patterns contain no shorter description than themselves—they resist interpretation. Meaning arises only when a pattern admits a compact interpreter I that reconstructs it predictively.
Thus, interpretation is compression. Truth becomes a measure of how coherently an interpreter maps a pattern to an outcome within finite resources.
6. The Conditional Turn
Conditionalism reframes the entire edifice:
When philosophers speak of “unconditional truth,” they implicitly assume a hidden universal interpreter—a divine Tarski model. Conditionalism simply removes that ghost.
7. The Meta-Interpreter
Every act of reasoning presupposes an interpreter evaluating another interpreter. Gödel’s self-reference and Turing’s halting problem show that a system cannot perfectly interpret itself. There is no ultimate vantage. Conditionalism makes peace with this: recursion without closure. Truth, like computation, is locally consistent but globally ungrounded.
8. Conclusion
Computation gives us syntax; Tarski gives us semantics; Gödel and Chaitin reveal the boundaries of both. Conditionalism unifies them under one rule:
Truth is not a property of statements, but of evaluations.
To compute is to interpret, and to interpret is to condition.
Every truth lives inside an interpreter. Outside interpretation, there is only unparsed chaos—patterns without meaning, syntax without truth.